An elliptic curve over a finite field $\mathbb{F}_{p}$ is defined by the Weierstrass standard equation:

Where $a$ and $b$ are constants that determine the shape of the curve.

These type of curves are used on crypto-systems like ECDSA (Elliptic Curve Digital Signature Algorithm) due to the difficulty of solving the ECDLP (Elliptic Curve Discrete Logarithm Problem).

1. Elliptic curves in cryptography

Elliptic curves have gained popularity over classical methods such as RSA because they offer an equivalent or superior level of security with significantly shorter key sizes. For example, a 256-bits key on ECDSA offers a security level comparable to 3072-bits RSA key (See Table 2 of NIST SP 800-57 Part 1 Rev. 5)¹. This results in significant savings in bandwidth, computational time, and storage space. Additionally, the ECDLP (Elliptic Curve Discrete Logarithm Problem) is considered harder to solve than the classical DLP (Discrete Logarithm Problem) in integers modulo $n$. As a result, with equal computational resources, elliptic curves provide a higher level of security.

2. Group structure in Elliptic Curves

For the construction of the algebraic structure used in ECDSA, we must define an abelian group over the curve.

2.1 Definition of an Abelian group

An abelian group is an algebraic structure ($\mathbb{G}, \oplus$), where:

• $\mathbb{G}$ is a non-empty set
• $\oplus$ is a binary operation defined $\oplus : \mathbb{G} \times \mathbb{G} \to \mathbb{G}$
  Which satisfies the following properties:
  • Associativity: $\forall a,b,c \in \mathbb{G}, (a \oplus b) \oplus c = a \oplus (b \oplus c)$
  • Identity element: $\exists e \in \mathbb{G} \mid \forall a \in \mathbb{G}, e \oplus a = a \oplus e = a$
  • Inverse element: $\forall a \in \mathbb{G}, \exists b \in \mathbb{G} \mid a \oplus b = b \oplus a = e$
  • Commutativity: $\forall a,b \in \mathbb{G}, a \oplus b = b \oplus a$

2.2 Construction

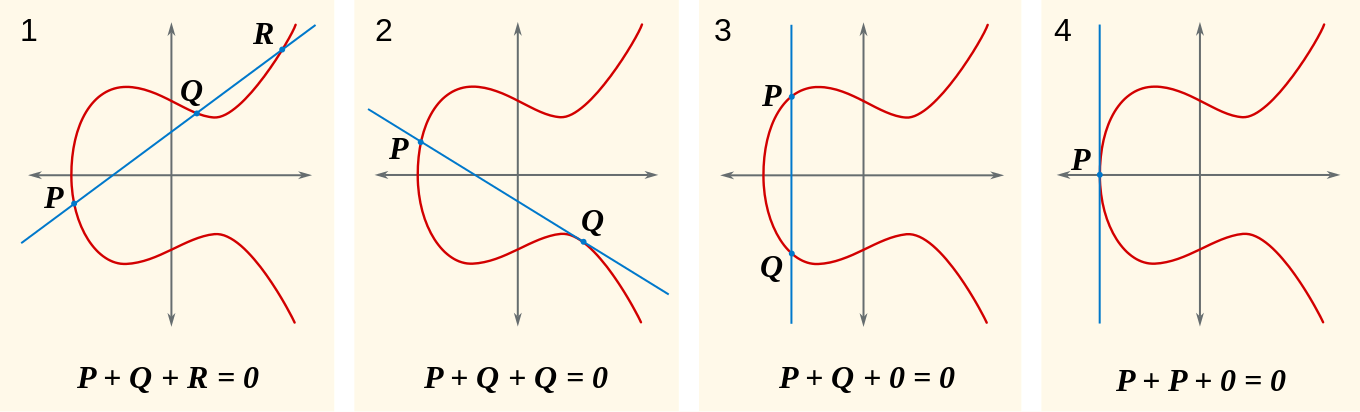
Over these elliptic curves, we define the algebraic structure of an abelian group as follows: Let $C$ be an elliptic curve over a field $\mathbb{F}_{p}$ defined by the Weierstrass standard equation

where $a,b \in \mathbb{F}_{p}$ and the curve is non-singular (i.e., it has no points with multiple tangents).
Consider the points $P = (x_{p},y_{p})$ and $Q = (x_{q}, y_{q})$ such that $P,Q \in C$ The binary operation $\oplus: C \times C \to C$ is defined as follows:

If $P \neq Q$ and $x_{p} \neq x_{ q}$:

1. Calculate the slope between $P$ and $Q$

2. Calculate coordinates of the point $R$

Thus:

If $P = Q$: the slope between $P$ and $Q$ is the derivative of the curve at $x_{p}$:

Taking the derivative:

Substituting $m$ gives:

We define a point $\mathcal{O}$ at infinity on the projective plane, this point satisfies the following properties:

If $P = (x, y)$ and $Q(x,-y)$ then:

The point $\mathcal{O}$ serves as the neutral element, ensuring the structure is an abelian group.

Scalar multiplication in this structure is defined as follows: Given a point $P \in C$ and a scalar $k \in \mathbb{Z}$:

3. The security of Elliptic Curves: ECDLP (Elliptic Curve Discrete Logarithm Problem)

The security on this signature scheme relies entirely on the ECDLP, which is defined as follows:

• Given an elliptic curve $C$ over the finite field $\mathbb{F}_{p}$, a generator point $G$ on the curve, and a point $P$ on the curve, find the integer $k$ such that $P = k \cdot G$

For carefully selected finite fields, there is not efficient solution to this problem.

Scalar multiplication on an elliptic curve over a finite field $\mathbb{F}_{p}$ is analogous to exponentiation in the multiplicative group $\mathbb{Z}_{p}$ (Integers modulo $p$), for example:.

mirrors the operation in $\mathbb{Z}_{p}$

Thus, the ECDLP is analogous to DLP (Discrete logarithm problem) in $\mathbb{Z}_{p}$.

However, the best known algorithms for ECDLP have roughly exponential complexity, unlike DLP in some groups where subexponential algorithms are known. As a result, breaking ECDLP is widely believed to be harder at equivalent key sizes.

Note that the difficult of ECDLP depends largely on the size of the field $\mathbb{F}_{p}$ and the rigorous selection of the curve, such as secp256k1.

4. Cryptographic keys in Elliptic curves

4.1 Private keys

Private keys are integers selected within the range of the curve size, generally are integers of 256-bit. The generation of these keys is extremely fast and efficient.

4.2 Public keys

The public keys are points on the elliptic curve, defined by their coordinates $(x,y)$. Due the properties of this family of curves, the points can be expressed in a compressed format using only a single coordinate $x$ and a flag indicating whether $y$ is positive or negative. Therefore, a 256-bit private key corresponds to a 257-bit public key.

4.3 Generator and order

On an elliptic curve $C$, a point $G$ (generator), an integer $n$ (order) are defined; $n$ represents the number of points over the curve. For a generator $G$, there exists an $r \in \mathbb{Z}^+$ such that $r \cdot G = O$ where $r \mid n$. This $r$ is called the order of the subgroup generated by $G$. $G$ is a generator of the entire group if $r = n$.

4.4 Key derivation

Given a elliptic curve $C$ and a generator point $G$, let $k$ be an integer (Private key). It is possible to compute a point on the curve.

This operation consists of summing the point $G$ with itself $k$ times.

Note that calculate $k$ given the points $G$ and $P$ is computationally infeasible because:

1. There is no defined inverse operation in the group that allows $k = \frac{P}{G}$
2. The only known methods to determine $k$ are through brute force or specialized algorithms, ensuring the security of the system.

This process is described in greater detail in Digital Signature Standard (DSS)²

5. ECDSA: Digital signatures with Elliptic Curves

It is important to use well-known and rigorously selected elliptic curves to avoid security breaches, such as the widely used secp256k1.

Below, we outline the ECDSA algorithm, based on Practical Cryptography For Developers³

5.1 Generation

The process for signing a message is as follows:

1. Compute the hash of the message ($m$) with SHA-256 (Secure Hash Algorithm) $h = \text{hash}(m)$
2. Generate a random integer $c$ in the range $[1, n-1]$ where $n$ is the order of the curve.
3. Compute the point $R = c \cdot G$. Take the $x$ coordinate of the point $R$ and assign it to $r$
4. Calculate the signature proof:

where $c^{-1}$ is the modular inverse of $c$ satisfying $c \cdot c^{-1} = 1 \text{ mod } n$ and $k$ is the private key of the signer.

5. The signature is the pair $(r,s)$

5.1.1 Considerations

Note that if the random number $c$ is generated with low entropy—meaning it is predictable or reused—the system becomes vulnerable to leaking the signer’s private key.

5.2 Verification

To verify the signature, the message $m$, the public key $P$ and the signature $(r,s)$ are taken as input. The process is as follows:

1. Compute the hash of the message ($m$) using SHA-256 (Secure Hash Algorithm) $h = \text{hash}(m)$
2. Compute the modular inverse of the signature proof $s^{-1} \text{ mod } n$
3. Attempt to recover the random point $R$ used during the signature. Define: $$R' = (h \cdot s^{-1}) \cdot G + (r \cdot s^{-1}) * P$$
4. Take the $x$ coordinate of the recovered point $R'$ as $r'$
5. The signature is valid if $r' = r$.

It is also possible to recover then public key $P$ from the signature.

5.2.1 Considerations

Note that finding $r$ and $s$ through brute force is totally infeasible.

5.3 Implementation

The following is an example of the ECDSA algorithm implemented in Solidity.

function verifySignature(bytes32 message, uint8 v, bytes32 r, bytes32 s) public view returns (bool) {
    bytes32 hash = sha256(abi.encodePacked(message));
    return ecrecover(hash, v, r, s) == msg.sender;
}

6. Conclusion

The elliptic curves offers high security and efficiency for cryptographic purposes due to their algebraic-geometric structure, which complicates the development of algorithms capable of solving the ECDLP quickly. On the other hand, ECDSA uses shorter keys than other equivalent systems, such as RSA, which has made ECDSA a standard in the cryptography industry.

6.1 References